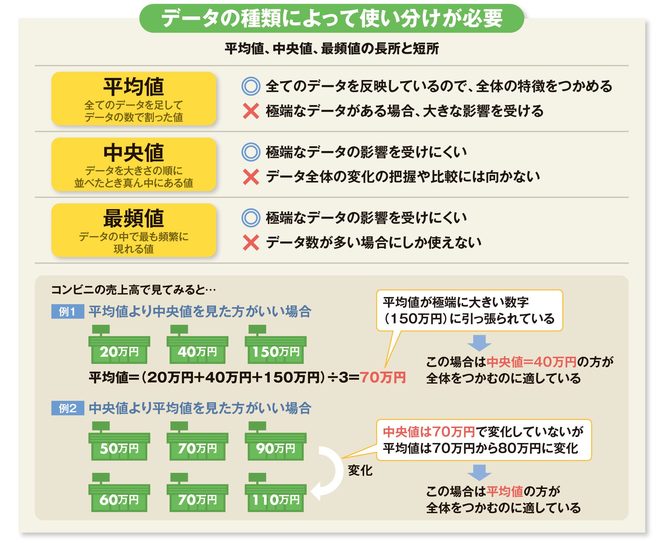
28中央値,最 さい 頻 ひん 値 ち 例 題 29測定値 1 年 キーポイント28 中央値(メジアン)は,資料の 値を大きさの順に並べたとき, その中央の値のこと。 度数分布表での最頻値(モー ド)は,度数のもっとも大き い階級の階級値である。 キーポイント29代表値 解説 各資料の値全体を代表している,つまり,資料全体の特徴を表している数値のことを代表値といい,次の3つがあります。 平均値(平均):資料全体の数値の合計を,資料の全個数で割って得られる値で,次の式により求めることができます。中学 資料の活用(解答) 目次 ページ 学習内容 11 度数分布 21 場合の数 22 確率の求め方 23 資料の活用のまとめ
Saiei School Com Wp Content Uploads 16 12 Teretama Math Ruidai Pdf
資料の活用 中央値 求め方
資料の活用 中央値 求め方-1 年 資料の活用 「貧困率」を改善するには ~国民生活基礎調査のデータの分布傾向から考える~ 分布の形・代表値(平均値・中央値・最頻値)・ヒストグラム 1.問題について 平成21 年10 月 日の新聞に以下の記事が掲載された。2.「資料の活用」領域のとらえ (1)「資料の活用」領域全体について かつて2学年に位置付いていた「資料の整理」では,数値の集合として与えられた資料をグラフ化 目的に応じて資料を収集し,コンピュータ を用いたりするなどして表やグラフに整理




資料の活用 中学生 数学のノート Clear
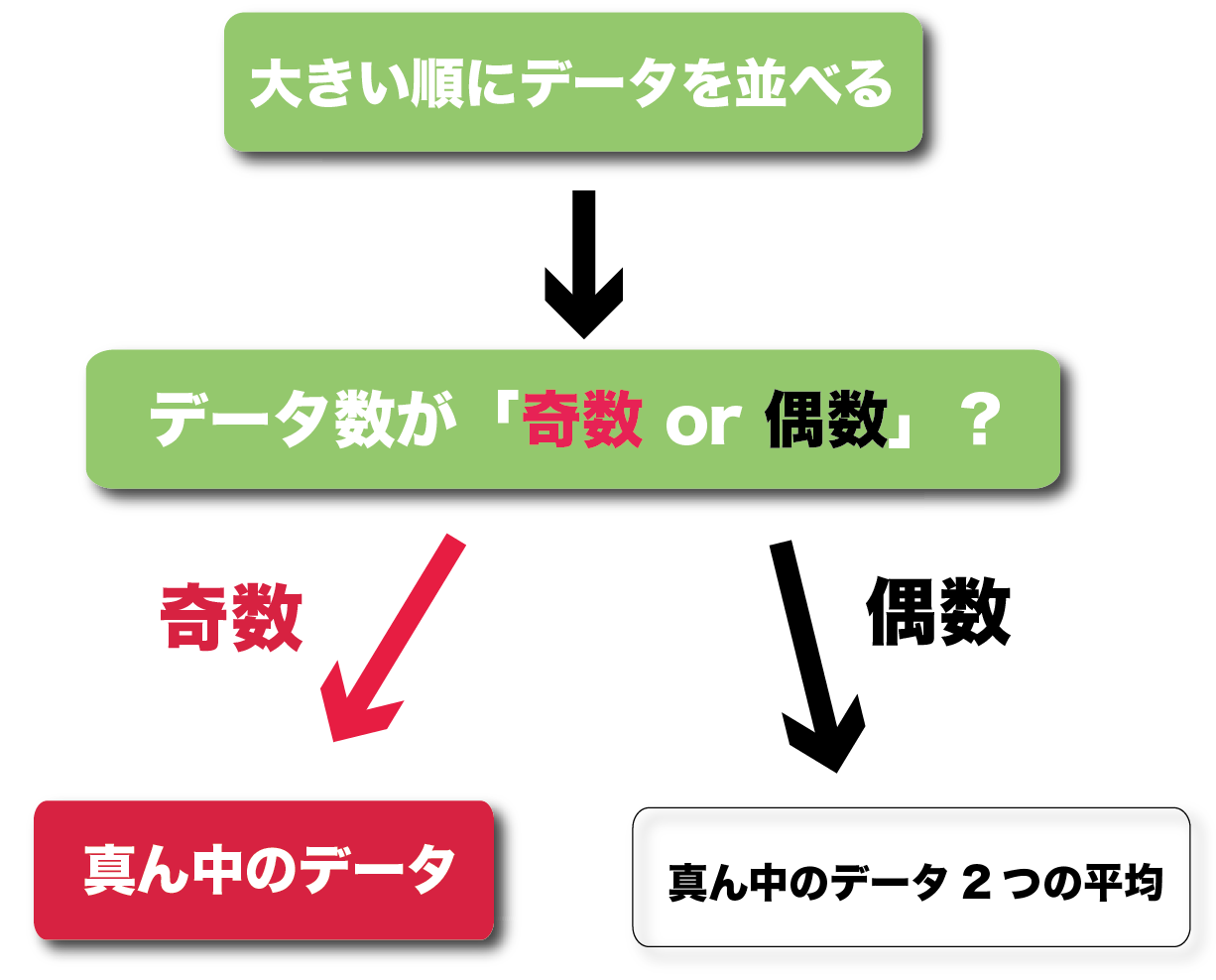
中央値資料の値を大きい順に並べたとき、中央の値を中央値(メジアン)といいます。奇数個の中央値例\(9\) 人の生徒の通学時間(分)\(6, 13 , 15 , 10 , 12 , 24 , 15 , 8 , 18 \)この \(9\) 人の通学時間の中央値を求めてみましょう。\(9\) 個のイ ヒストグラムや代表値を用いて資料の傾向をとらえ説明すること。 〔用語・記号〕 平均値 中央値 最頻値 相対度数 範囲 階級 内容の取扱い (6) 内容の「D資料の活用」の(1)に関連して,誤差や近似値,a×10n の形の表現を取り扱 うものとする。領域D「資料の活用」 単元(1) 資料の分布 本単元のプリント集の問題は、以下の2つに分類されています。 ヒストグラムや代表値の必要性と意味を理解すること ヒストグラムや代表値を用いて資料の傾向をとらえ説明すること
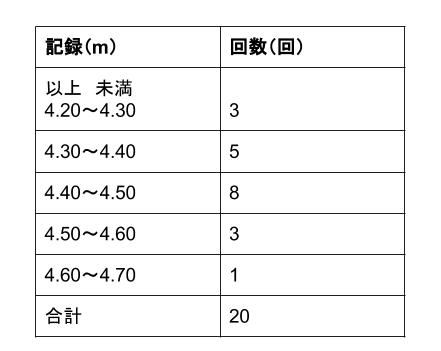
中央値(ちゅうおうち、英 median )あるいはメジアン、メディアンとは、データや集合の代表値の一つで、順位が中央である値のことである。 ただし、データの大きさが偶数の場合は、中央順位2個の値の算術平均をとる。 中間値の定理の「中間値」はこの中央値の意味とは異なる。の資料の妥当性について調べようとして いる。 平均値,中央値,最頻値につ いて理解し,状況に応じて適 切な代表値を用いる必要が あることを理解する。(2) る。 エ①代表値の必要性と意味を理解してい ウ②問題を解決するため,平均値や中央値② 中央値 度数分布表から中央値を求める場合、まん中の順番にくる資料が入っている階級の階級値 が中央値となります。 中央値は、10 番目と11 番目の人がはいる階級、40cm以上45cm未満の階級の階級値とな るので 425cm ③ 最頻値
87 そこで,本研究では中1の「資料の活用」領域,つまり「資料の散らばり と代表値」単元に焦点を当て,研究の目的を次のように設定する。 研究の目的 統計的思考力の育成を目指した中1の「資料の散らばりと代表値」単元3 代表値(平均値,中央値,最頻値) 2時間 4 資料の活用(資料の活用,コンピュータを用いた統計処理) 3時間 (本時3/3) 5 近似値の有効数字(近似値,真の値,有効数字) 1時間 6 学習のまとめ1年「資料の活用」 氏名 階級 (g) 度数(個) 50 以上 ~ 60 未満 3 60 ~ 70 5 70 ~ 80 2 計 10 ※コンピュータを利用して資料を整理することもできます。 平均値(Average) 中央値(Median) 最頻値(Mode) 最大値(Max) 最小値(Min) ・ 階級ごとに、その度数を表した表を 度数分布



世界四季報 中1数学 資料の活用 中央値の求め方 Youtube T Co Ccfwdf7bgp 中央値の求め方の記憶がすっぽり抜けていたんだけど習っていなかったのかな T Co Ibn9m11mmm Twitter
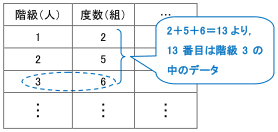



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座
資料を大きさ順に並べたときの中央の値を 中央値 または メジアン いいます。⑩⑪統計資料 の活用Ⅱ 活用問題③ ⑩⑪統計的手法を活用して,問題を解決する。 ㋐ ㋐ ㋑ ㋒ 12 ⑫章の問題 ⑫教科書p250に取り組む。 3 本時案 (1)本時の目標 代表値の意味を理解し,資料から値を求めることができる。これだと,7人の記録の中央値にな ってしまうから,9人の記録の中央 値にしないといけません。 表 (以下 裏 ワークシート活用場面例 ポイント 先生 中学校 指導資料 「課題チャレンジ 代表値を正しく読み取ることができるようにしよう」では,ただ単に用語




中学数学 資料の散らばりと代表値




中1資料の活用 中学生 数学のノート Clear
「資料の活用」の1学年の内容に焦点を絞って, (平均値,中央値,最頻値)や範囲について,第5節では, 統計調査の大まかな計画について,第6節では,モード アベレージ 中央値 階級値 近似値 1つの階級に入っている資料の個々の値はいろいろだが、 どの値もすべてその階級の(① )と考えて計算する。 2 まさおみさんの所属する陸上部員11人の50m走の記録(秒)は、次のようでした。1 単元名 資料の散らばりと代表値 2 単元の目標 ・資料を度数分布表やヒストグラムに整理したり、代表値や範囲などを用いたりして、資料の傾向や特徴 をとらえ意欲的に数学を問題の解決に活用しようとしている。(関心・意欲・態度)




資料の活用 中学生 数学のノート Clear




中学数学 資料の散らばりと代表値
資料の活用 代表値(1) 175 範 囲資料全体の散らばり具合を表す数値のこと。 (範囲)=(最大の値)-(最小の値) 代表値資料全体の特徴を、1つの数値で表したもの。 ・平均値 個々の資料の値の合計を、資料の総数でわったもの。 最頻値(モード)の求め方 を知っていると便利。 資料と活用の問題がとけるし、 日常生活でもつかえるようになるんだ。 今日はそんな便利な、 最頻値(モード)の求め方 を2ステップで解説していくよ。 よかったら参考にしてみてね^^293 中1数学 資料の活用 資料の活用で、単位をつける時とつけないときがありますが、それはなぜですか? 最頻値や中央値、平均値などが聞かれたら単位をつける、階級値などだったら単位はつけない、という考え方でいいのですか?



中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ




中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
・資料の分析に関する平均値 など <数学科>(第1学年 単元名「資料の活用」) 学習指導略案 「階級値」「中央値(メジアン)」「最頻値(モード)」などが共通理解しておくことが必要である。代表値には 「平均値」「中央値」「最頻値」「範囲」 などがあります. 「真理は1つだけでなければならない」などと決めつけてはいけません.どの代表値も長所短所があり,各自が資料を使って分析したいときに,ねらいを実現するために一番適した代表値に関心をもち,平均値や中央値,最頻 る。行動の観察 3 ・ 4 整理・分析 資料の範囲を調べたり, 度数分布表に整理する。 また,その分布の様子な どから資料の傾向を読み 取る。 資料の最大値・最小値,範囲の意味や,度数 分布表の必要性と




ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に



これの中央値 最頻値 平均値の求め方を教えてください 中央値とは言 Yahoo 知恵袋
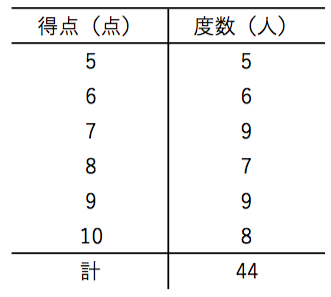
中央値は,資料の数が偶数だか ら,中央2つの数の平均を求め るので, でした。 度数布表から,Aのルートの 最頻値は で,Bのルートの最 頻値は だったよ。 資料全体の度数が違うものを比 較するときには,相対度数を求 めると資料の傾向が読み取れる第1学年 7 資料の活用 数学的な思考力・判断力・表現力を育む問題解答 年 組 号 氏名 練習問題③ (1) 0 m以上250 m未満の階級 ポイント 中央値は,大きい順に並べた中央の値だね。 この資料は偶数だから,25 番目と26 番目中央値(メジアン) 資料の値を大きさの順に並べた時の中央の値を 中央値(メジアン) という。 例 生徒25人の身長の中央値は低い方から13番目の人の値となる(高い方から数えても13番目で同じ)。 生徒数が24人の場合、12番めと13番目の2人の値の平均となる。




度数分布表から平均値と最頻値を求める 苦手な数学を簡単に




中央値 最頻値 中1数学 資料の活用4 Youtube
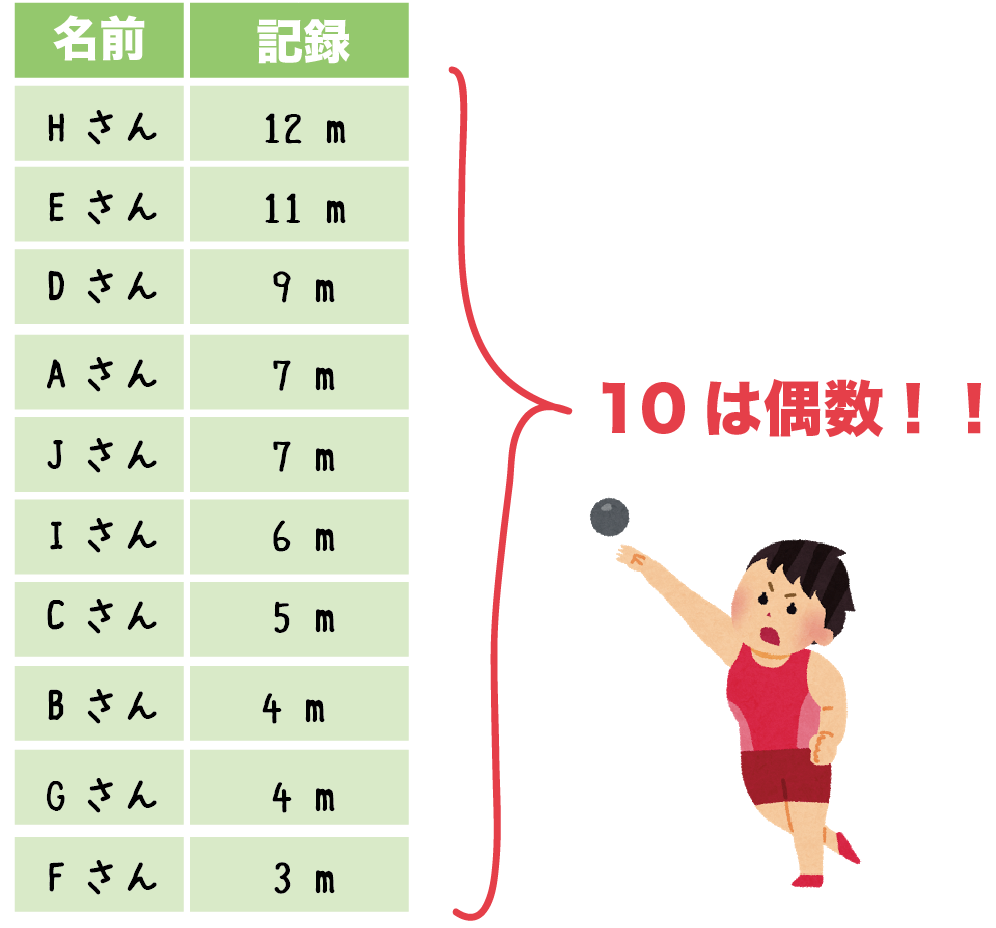
14 Prisola International Inc 1 中学1年数学講座 第7章資料の活用 (4)中央値・最頻値 基本問題 講師:高山よしなり〔用語・記号〕平均値 中央値 最頻値 相対度数 範囲 階級 目的に応じて資料を収集し,統計的な処理を行うことによって傾向をよみ取り,説明することの中でも,1年の学習では,文字通り「資料の活用方法」を学ぶことになる。中央値(メジアン)とは,資料の値を大きさの順に並べたとき の中央の値のことだね。 試合数が試合(偶数)の場合,中央値は,得点が少ない 順に並べたときの10・11試合目の得点の平均値になるよ。 資料の個数が奇数の場合 ↑




中1 数学 中1 87 代表値と散らばり Youtube




中1 数学 資料の整理4 平均値と中央値 12分 Youtube



2



Saiei School Com Wp Content Uploads 16 12 Teretama Math Ruidai Pdf




中学数学 資料の散らばりと代表値




中学数学 資料の分析と活用 資料の整理 問題まとめ集 全国公立高校過去問解説集 わかりやすさに徹底的にこだわっています 教育 学習 受験 自宅でできる受験対策ショップ ワカルー Wakaru
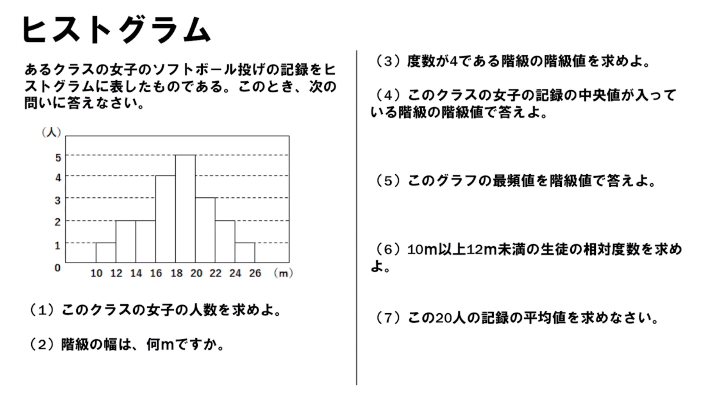



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu



中央値について 真ん中の落とし穴に気をつけろ 苦手な数学を簡単に



中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2



1
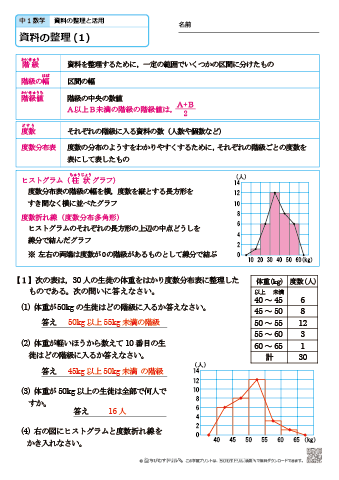



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



資料の活用で中央値の階級がどこに入るか という問題の仕方を教えてくださ Yahoo 知恵袋




全国学力調査 埼玉県の中3ができない数学の内容は 2 ブログ アビット
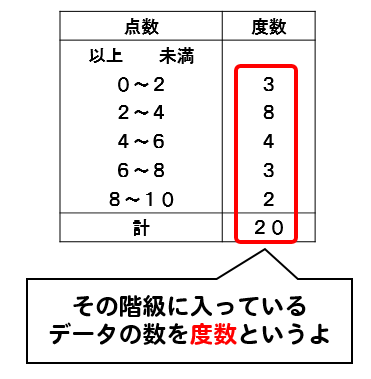



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



中学校数学 資料の活用 で学ぶ 中央値について質問です 資料が Yahoo 知恵袋




中学校数学1年 資料の活用 代表値と散らばり 最頻値まで Youtube
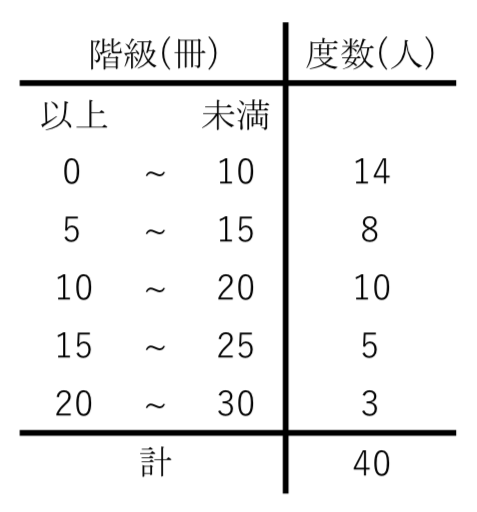



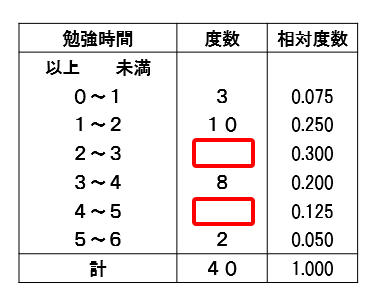
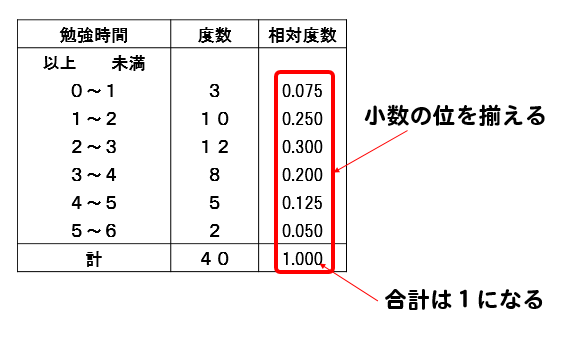
度数分布表から相対度数を求める 苦手な数学を簡単に




受験対策 数学 資料の活用 Youtube
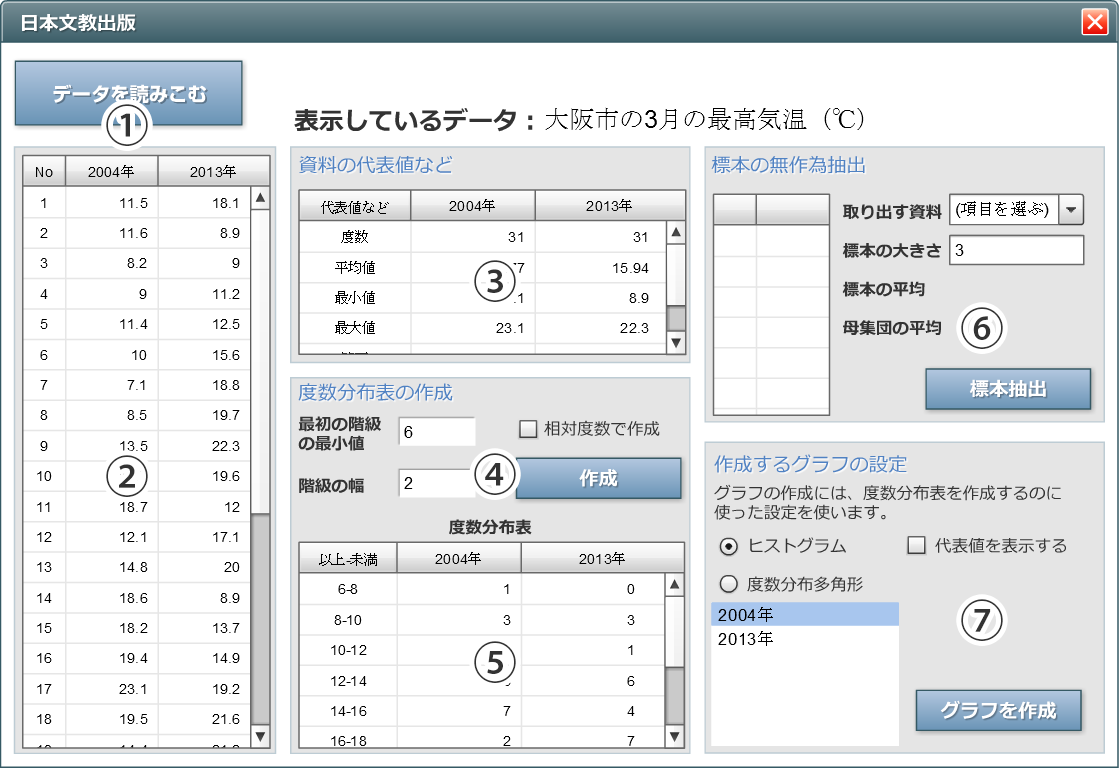



資料の活用コンテンツ Exhist お役立ちツール 日本文教出版



2
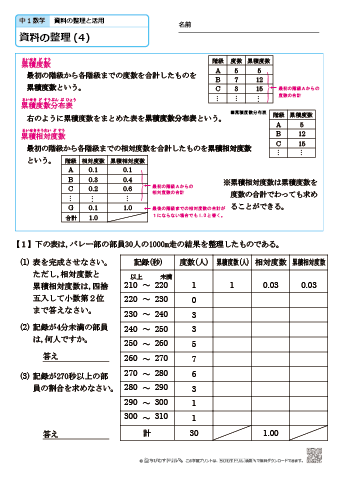



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 資料の活用 重要語句 中学生 数学のノート Clear




高校受験対策 資料の活用 最頻値と平均値 の問題 動画 19ch



Q Tbn And9gcrucc9oonrnsr8xt7hwgg24wwhri7 M4v0tilyyttjwqnmgepnl Usqp Cau
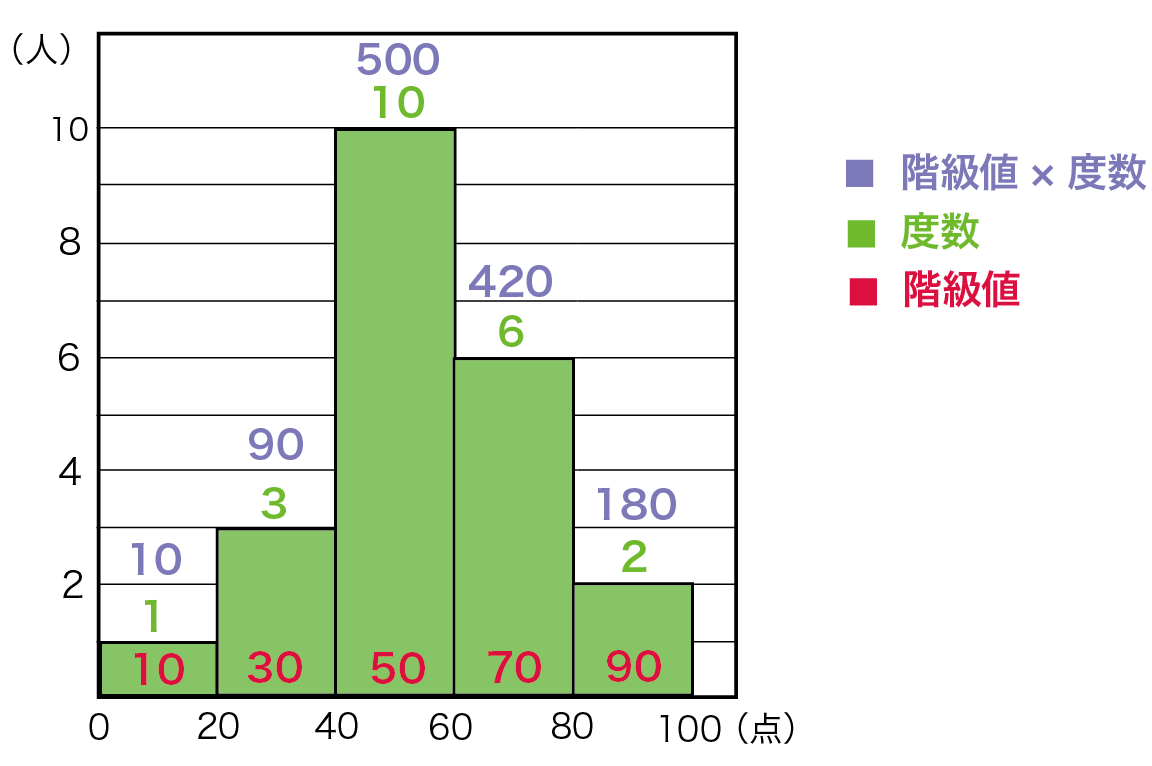



資料の活用 Qikeru 学びを楽しくわかりやすく




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




資料の活用 中1数学 中3総合a対策 しおちゃんの元氣アップ ココロのサプリ




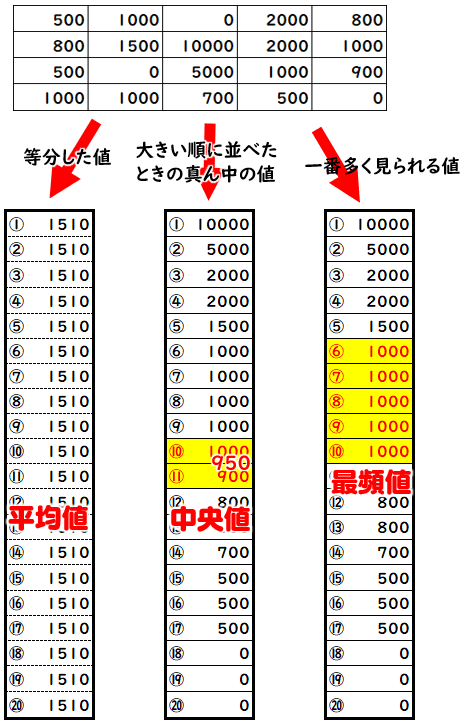
代表値 平均値 中央値 最頻値 の意味と違い 数学fun
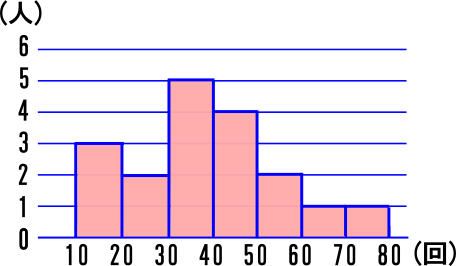



中学1年数学練習問題 代表値 平均値 階級値 中央値 最頻値の問題
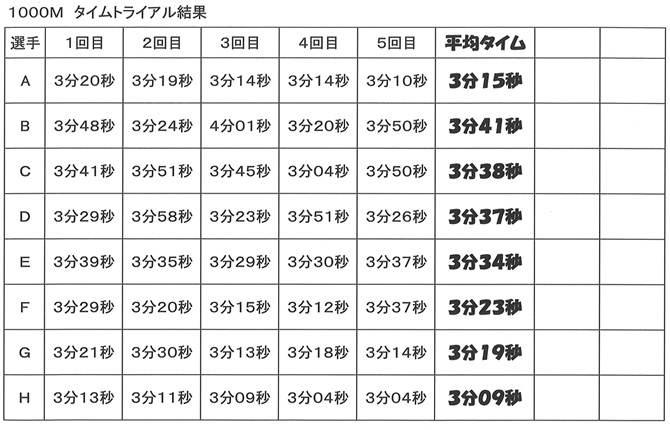



授業実践記録 数学 資料の活用 啓林館




世界四季報 Sur Twitter 中1数学 資料の活用 中央値の求め方 Youtube T Co Ccfwdf7bgp 中央値の求め方の記憶がすっぽり抜けていたんだけど習っていなかったのかな




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく




中3の実テ過去問の 資料の活用についての問題です Clear



Http Www Pegasus Fc Com Teachingaid Mathpdf Keyword Ans 06 1 Pdf




高校受験対策 資料の活用 中央値 の問題 動画 19ch




中1数学 資料の活用 中央値の求め方 Youtube




中1数学 資料の活用のポイント練習問題
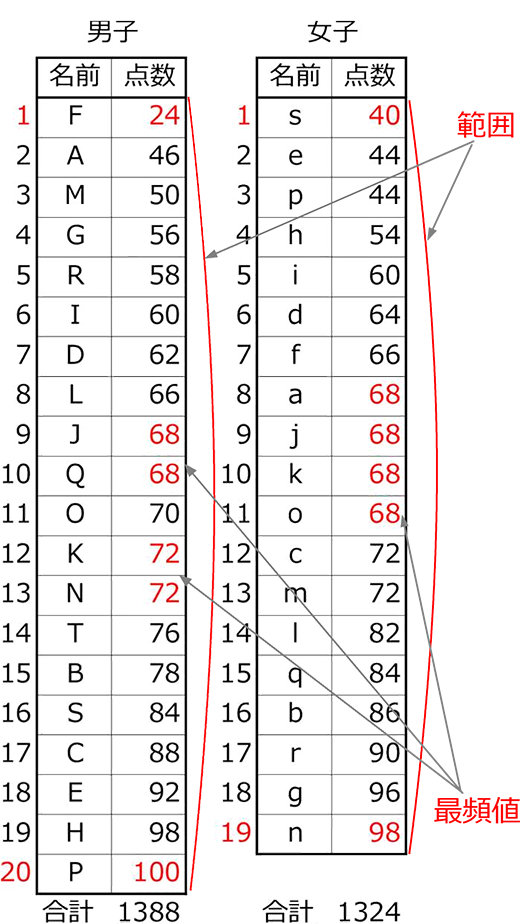



中学数学 資料の散らばりと代表値



無料 中1数学 基本解説 問題プリント 資料の活用2 近似値 145



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




世界一わかりやすい数学問題集中1 7章 資料の活用




世界四季報 Sur Twitter 中1数学 資料の活用 中央値の求め方 Youtube T Co Ccfwdf7bgp 中央値の求め方の記憶がすっぽり抜けていたんだけど習っていなかったのかな




中1数学 資料の活用 中央値 資料の総数が偶数の場合 Youtube



1



1
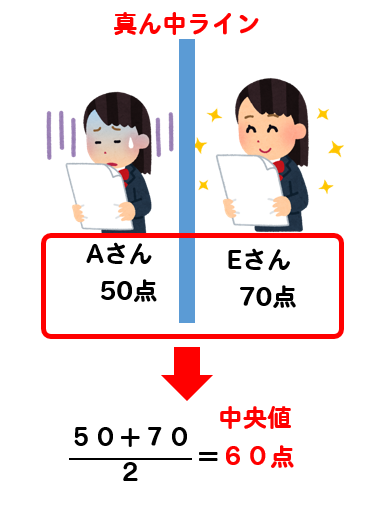



中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ




中学数学 資料の分析と活用 資料の整理 問題まとめ集 全国公立高校過去問解説集 わかりやすさに徹底的にこだわっています 教育 学習 受験 自宅でできる受験対策ショップ ワカルー Wakaru



中学校の数学の 資料の活用 は何年生でならうのでしょうか 階 Yahoo 知恵袋
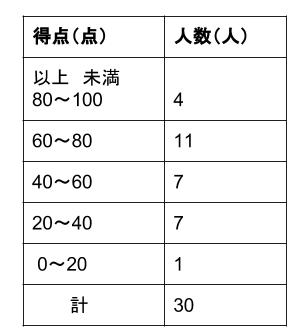



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su
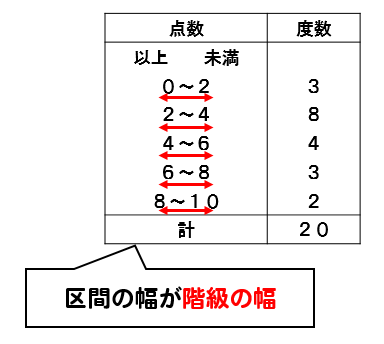



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1数学 資料の活用のポイント練習問題




中学数学 3つの代表値の求め方 Qikeru 学びを楽しくわかりやすく



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su




中1数学 資料の活用 中央値 資料の総数が偶数の場合 Youtube



中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 資料の分析と活用 資料の整理 問題まとめ集 全国公立高校過去問解説集 わかりやすさに徹底的にこだわっています 教育 学習 受験 自宅でできる受験対策ショップ ワカルー Wakaru




小学6年生の算数 資料の調べ方 度数分布表 柱状グラフ 練習問題プリント ちびむすドリル 小学生



代表値 平均値 中央値 最頻値 の意味と違い 数学fun




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
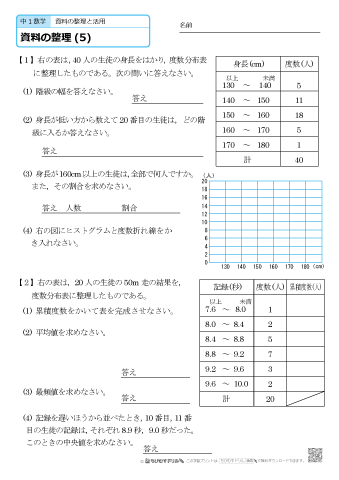



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




度数分布表から平均値を求める 中学1年の数学 身勝手な主張




メジアン と モード 中学数学 資料の活用 をファッションでおぼえる 愛知県安城市の個別塾 学習塾 ナビ個別指導学院 安城南校ブログ




これで点が取れる 単元末テスト中1数学 7章 資料の活用




中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



資料の活用 教遊者




Wfjx75art1hxrm



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ




2 解答見ても分からないので教えてください Clear




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット



資料の活用で このような度数分布表から簡単に中央値を求める方法はありますか Yahoo 知恵袋



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



中学数学 資料の散らばりと代表値



Www Chuo Tky Ed Jp Ginza Jh Resources Content 0513 Pdf



中学 相対度数の計算方法と問題はこれでバッチリ 数スタ




高校受験対策 資料の活用 中央値 の問題 動画 19ch




中学数学 資料の散らばりと代表値




鹿児島市立福平中学校




中1数学 資料の活用 の重要ポイントをピックアップし 勉強方法を紹介 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 数字 資料の活用 絶対攻略 中学生 数学のノート Clear
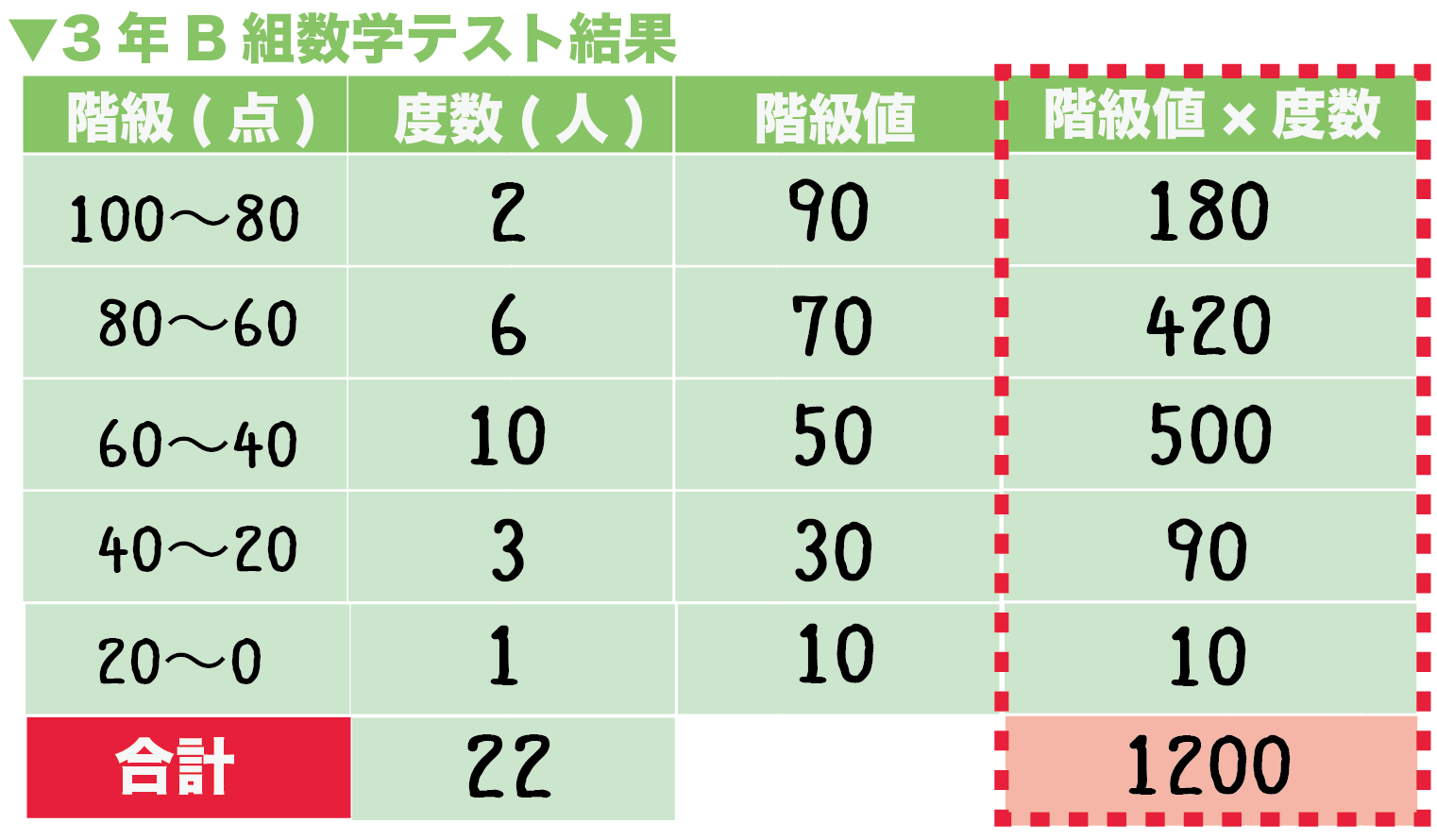



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中1 7章 資料の活用
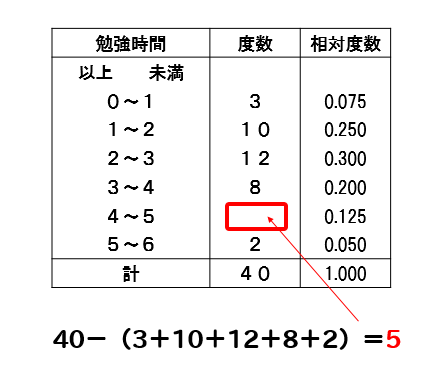



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




代表値と散らばり 数学の要点まとめ 練習問題一覧



中央値の求め方 中学1年数学 資料の分析と活用




中1数学 資料の活用 中央値の求め方 Youtube




平均値と階級値について 苦手な数学を簡単に




資料の活用の単元全然わからないのですが教えてください Clear



0 件のコメント:
コメントを投稿